Summary:
We can now test for a mutation that was strongly associated with SAS in an experiment presented at the NCA National Specialty. The experimenters suggest that SAS in the Newfoundland is largely an autosomal dominant with incomplete (80%) penetrance. A breeding recommendation was given that we not eliminate heterozygotes immediately for fear of losing genetic diversity in our small population. Instead, heterozygotes would be bred only to clears and we would use the 50% genetically clear dogs resulting to continue breeding. In contrast to the strategy of breeding recessive carriers (also heterozygotes) we would be doing breedings in which we would expect 40% of the offspring to be affected. With recessives (say cystinuria) we can breed carriers to clears without ever producing affected dogs. The Breeders Education Committee has discussed these recommendations and the study and conclude: a) a good estimate of penetrance is an important factor in deciding on a breeding recommendation, b) with a penetrance as high as 80% we might be better advised to eliminate the gene (not breed heterozygotes) since the cost to diversity would be small, and c) The 80% value presented is very much in question. These considerations are important for the future of genetic testing in our breed since many future tests will probably be for genes that “increase the risk” of a disorder, rather than simply causing it, i.e. incomplete penetrance.
Recessive Strategies
Generally when a mutation is discovered to be responsible for a recessive disorder, breeders are advised to breed carriers that are otherwise superior specimens to clears. The outcome of such a breeding will be half clear and half carrier with no offspring actually showing the disorder. In some cases even affecteds may be bred to clears, producing a litter of all carriers. Over time it is hoped that carriers will be replaced by younger clear animals of at least equal quality, since carriers will be moderately less attractive for breeding than clears. As long as we never breed affected or carriers to other carriers we need never produce the disease. This is, for example, the NCA policy on the breeding of cystinuria carriers. There are sound reasons for using this strategy. When a recessive disorder is first recognized as being present, the allele causing it is often already well-established in the population. Suppose breeders start realizing something is wrong when 1 out of 100 in the population are affected. It's certainly not unreasonable that it would take that incidence to get our attention. We have no formal surveillance looking for new problems and certainly have no coordinated efforts to deal with them when they occur. Also, many disorders are relatively variable in the age at which they are detectable. Even cystinuria in a dog would not be recognized until an acute episode (usually urinary blockage) and although all affected would show elevated cysteine in the urine, not all would have a noticeable clinical problem. It is reasonable therefore, that 1 out of 100 dogs might have cystinuria or something like it before we recognized that it was present. At this point, we can calculate from Hardy-Weinberg equilibrium, that on the order of 18% of the population would already be carriers (heterozygotes.) If a DNA test is developed at this point, eliminating carriers would represent an instantaneous, substantial reduction in the breeding population (not good if this population is small) and the elimination of many superior dogs that have no health problems themselves. Note that if 10% of the dogs were affected, 43% of the population would be carriers representing 48% of the unaffected dogs. We would be losing many potentially important alleles in the population were we to take a draconian position of not breeding any carriers. The strategy of breeding carriers to clears and the gradual reduction of carriers then allows an orderly elimination of the undesirable gene without eliminating a large chunk of the genetic diversity in the breed and without causing enormous loses in individual breeding programs.
Dominant/Incomplete Penetrance
Now let's contrast this with the situation that we apparently have with SAS. The current evidence points to SAS being inherited as a dominant trait with incomplete penetrance. This means that it's a dominant trait, but that not all dogs having the unfavorable genotype will actually develop the disease. In some sense, this is the worst of all possible worlds--only one parent need contribute a gene to produce the disorder in offspring, but (like recessive problems) we will also have a population of dogs that can pass on the disease to offspring but do not have it themselves, i.e. they are hidden. In the absence of a genetic test we will not know whether the sire, dam, or both passed on the gene to affected offspring. The strategy here has to account for the penetrance. Low penetrance will produce fewer affecteds, but will have more unidentified "carriers". High penetrance will produce many SAS offspring, but those with the gene are likely to actually have the disorder themselves, i.e. they will not be hidden. Now with SAS Stern estimates that we have 80% penetrance, i.e. 80% of the dogs with the unfavorable genotype (either homozygous or heterozygous) will be identifiable, because they will actually have SAS.) Virtually all responsible breeders do cardiologist screening of puppies, and more importantly of breeding stock. Many are doing dopplers on breeding stock to avoid the (hopefully small number of) dogs that are missed on auscultation, but detectable by doppler. So what could change with a genetic test is the elimination of the 20% of those with the SAS genotype that don't show the disease. They are now being bred. Many of these will be caught by progeny testing after they have a litter or two. If a dog consistently has SAS offspring with unrelated mates, we would probably stop breeding him or her. Now (assuming everything holds up on critical review) we have a "test" for this SAS mutation. It should be possible to eliminate SAS (at least that due to this mutation) in a single generation. But we need to evaluate the cost of doing this. Dr. Stern, in his presentation at the NCA National Specialty, gave the following recommendations: 1) Negative homozygous dogs will not pass on the gene and could be bred, 2) positive homozygous dogs should not be bred, and 3) positive heterozygous dogs should only be bred to clear dogs. Interestingly, this is nearly identical to the usual recommendation for recessive disorders. We need to ask the question: would it represent an important loss of diversity to simply eliminate the dogs carrying the mutation from the breeding pool? There is an important distinction between this situation and the recessive inheritance situation, in which unaffected carriers are likely to represent a substantial and undetectable reservoir of the mutation. Remember, very few responsible breeders are actually breeding SAS affected dogs. For all practical purposes, they are already eliminated regardless of the availability of the DNA test. So the only dogs in question are those who are truly SAS negative, but genotype positive. How many dogs are these? Taking the number of SAS diagnoses in the recent OFA/CTMB survey (around 2.7%) we would have approximately 0.6% dogs with the SAS genotype without the disorder. Many feel this is a substantial underestimate so suppose, for example, that we have 10% affected dogs in the population (these already will not be bred). If this were a recessive trait we would expect to have 48% of the unaffected dogs being carriers. With the 80% penetrant SAS we would expect to have slightly less than 2% of the potential breeding population being hidden carriers, now detectable by DNA test. Clearly, eliminating 1.8% of the unaffected dogs would be a lot less damaging than eliminating 48% of the unaffected carriers in the recessive inheritance scenario. So the cost of eliminating these dogs is fairly minimal. What is the cost of applying the recommendations given at the national? We would be doing breedings (heterozygous to homozygous negative) that we know are expected to produce at least 40% SAS affected puppies. This so that we can get our hands on those having the "clear" genotype (which we have to test for and which we are not guaranteed to get at all, let alone in the puppies that are otherwise promising). It certainly appears that it may be worth refraining from breeding this small percentage of dogs to rid ourselves of this gene in a single generation. In spite of the fact that breeding has not been random, the mass selection we have been doing over the past several generations would actually reduce the number of non-affected heterozygotes, not increase them and it would still be true that the great majority of dogs carrying the gene actually have SAS and would not be bred in any case.
Possible Pitfalls
First, Pattern of Inheritance: It is important that we have the pattern of inheritance correct. As you see above, 80% penetrance of a dominant characteristic is astronomically different than a recessive disorder. Further, there would be substantial differences in the cost of removing all the heterozygotes from the breeding pool depending upon the penetrance value. With high penetrance, say the 80% claimed, as we have seen most of the heterozygotes actually have SAS and are not being breed anyway. However, with low penetrance, say 20%, only one out of 5 heterozygotes actually have the disease, the others are hidden. So with a 2.7% disease rate, we would be eliminating roughly 10% of the breeding pool when we eliminated the silent heterozygotes. Possibly an acceptable cost to genetic diversity, but certainly far greater than when we have with 80% penetrance. However, we would produce substantially fewer SAS puppies as a side-effect of breeding the heterozygotes to clear dogs—as Dr. Stern suggests.
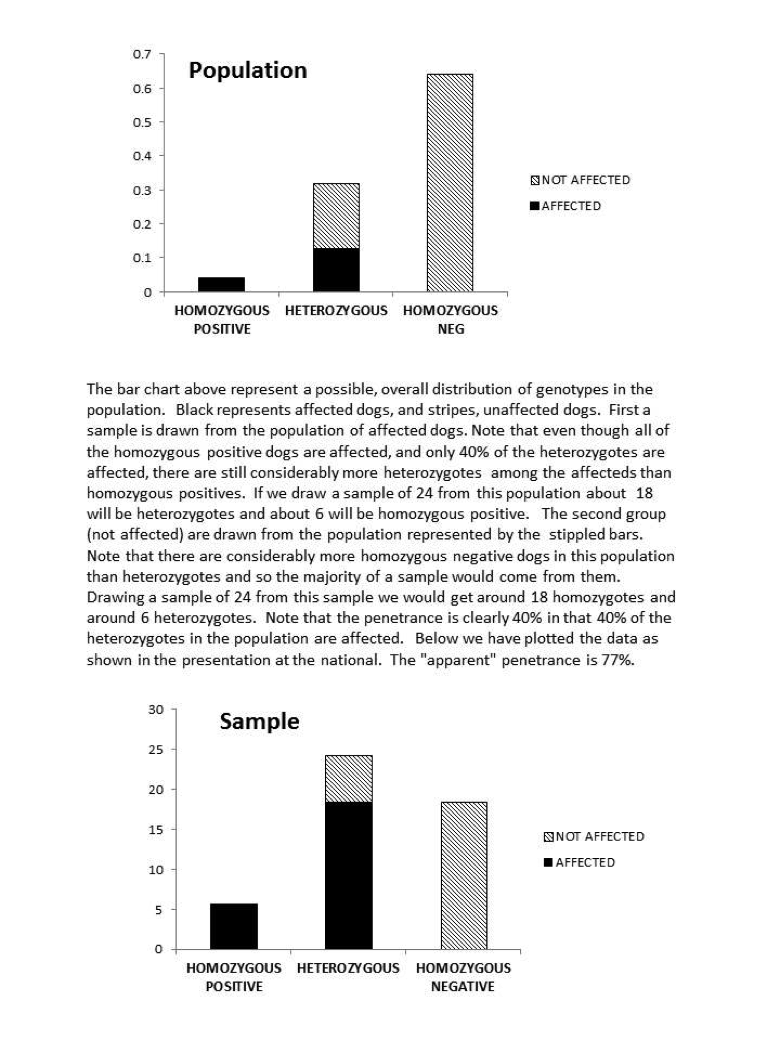
It is, in fact, highly possible that 80% is a substantial overestimate of the true penetrance. The estimate came from the fact that 80% of the heterozygotes in the study were affected. We have to realize, however, that this was not a random sample of heterozygote dogs. If it were, the straight forward ratio would give us an unbiased estimate. Instead, the experiment consisted of a sample (24) of SAS affected dogs and 24 unaffected. Now even if we were breeding randomly, there would be many more heterozygotes than homozygote positive dogs in the population. So basically, the SAS sample would consist of maybe 90% heterozygotes and 10% homozygote positive (will ignore for the time being the single homozygote negative dog with SAS). Clearly when you sample from that population, you’re going to get a lot of heterozygote, affected dogs. Now, there are also, almost undoubtedly considerably more homozygous negative dogs than heterozygotes in the unaffected population. A random sample of the unaffected dogs would then not have very many heterozygous dogs. It would look, therefore, as if almost all of the heterozygous dogs were affected. This is an artifact of the make-up of the two samples, not a result of high penetrance. We might ask if a pattern of genotypes sufficiently extreme to cause this distortion is likely. As an example, suppose we were to start with the horrible situation of random breeding and equal numbers of the normal and SAS mutant allele. After just one generations of avoiding breeding only the affected dogs we would have with 80% penetrance a population 4% homozygous positive, 32% heterozygous, and 64% homozygous negative. Clearly a random sample from a population of only affected dogs (the 4% homozygous + 80% of the heterozygotes) would have a preponderance of heterozygotes, and a random sample of unaffected dogs (20% of the heterozygotes and the entire homozygous negative group (64% of the entire population) would have a majority of homozygous dogs. The “apparent” penetrance (gotten by dividing the number of the affected dogs by the total number of heterozygous dogs across the two samples) would be 90.4%. If we had the same proportion of genotypes and a penetrance of 0.4%, the apparent penetrance would be 76.7%. Although this value is affected somewhat by penetrance, it is really most reflective of the current genotype distribution. With genotype distributions that reflect any selection against affected dogs, it will be a, possibly gross, overestimate. Remember, this is not a random sample of heterozygous dogs, but a sample with equal numbers of affected and unaffected dogs. A summary of the origin of this problem along with graphs of the population and sample distributions is at the end of the article. We encourage you to take a look.
Second, other genes: We have the other possible SAS gene or genes accounting for the single animal in the study that was homozygous for the normal allele, but had SAS. Is it possible that this was a false positive Doppler, rather than an example of another gene? We also don't have much information about the relative allelic frequencies of the two in the breed at large. It is possible, for example, that even though present in the study population in very small numbers, this gene might be important in the overall population (in fact theoretically, it could be responsible for much of the SAS in the dogs with the identified mutation as well).
Finally, accuracy of auscultation and doppler: We have little data on the false negative rate of auscultation relative to doppler. Most current screening is done in sequence, i.e. a positive finding of a murmur on auscultation is followed up by a doppler while an auscultation clearance is most often not. Thus a substantial false negative rate on auscultation could lead directly to an inflated number of “hidden” carriers of the SAS mutation: hidden, not because they do not have SAS, but because it was not detectable by auscultation. Lastly, we do not know very much about the reliability (repeatability) or the validity (how well does it detect SAS) of the doppler relative to necropsy. We would hope that the false negative doppler rate would be sufficiently low as to simply augment the apparent unaffected, genotype positive, dogs to a very small degree.